Cinématique - Mouvements, Positions et Trajectoires

On appelle trajectoire du point \((M)\) d'un solide \((S)\) l'ensemble des positions occupées successivement par ce point, au cours du temps, au cours de son déplacement par rapport à un référentiel donné.

Notation : \(T_{M \in S/R}\) désigne la trajectoire du point \(M\) appartenant à \((S)\), par rapport au repère \(\mathcal{R}\).

Soit une bicyclette en mouvement sur un plan horizontal par rapport à un repère \(\mathcal{R}_0\) lié au sol et considéré comme un repère fixe.

Soit le point \(A\) appartenant à la roue \(1\), point de contact entre la roue \(1\) et le sol \(0\).

Soit le point \(B\) appartenant au cadre \(2\), centre de l'articulation entre la roue \(1\) et le cadre \(2\).

Soit \(C\) un point appartenant à une poignée de frein.

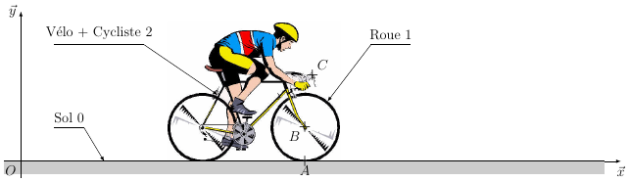
Question :

Déterminer et tracer les trajectoires suivantes :

\(T_{C \in 2/0}\) :

\(T_{B \in 2/0}\) :

\(T_{A \in 2/0}\) :

\(T_{B \in 1/2}\) :

\(T_{A \in 1/2}\) :

\(T_{B \in 1/0}\) :

\(T_{A \in 1/0}\) :